Сколько комбинаций из 5 чисел. Секреты везения или пошаговый алгоритм выигрыша в лотерее. Основная формула комбинаторики

Многие любители лотерей задаются вполне справедливым вопросом, как выиграть в лотерею 5 из 36. Прежде чем мы попытаемся ответить на эти вопросы необходимо ознакомится с правилами и посчитать вероятность выигрыша в лотерею 5 из 36.

Лотерею Гослото 5 из 36 можно назвать разумным выбором из всех существующих лотерей в данный момент, поскольку эта лотерея имеет максимальные шансы на выигрыш главного приза.

Конечно, говоря о максимальных шансах, мы должны понимать, что это лотерея и шансы на основной выигрыш джекпота не велики.

Количество комбинаций в лотереи 5 из 36

Логично будет перейти к фактам и озвучить точные цифры. Количество комбинаций лотереи 5 из 36:

376992
триста семьдесят шесть девятьсот девяносто два

и лишь одна из них становится выигрышной.

Мы выше писали, что игроки в 5 из 36 поступают разумно – потому, что по сравнению с лотерей Гослото 6 из 45, здесь шансы выиграть суперприз почти в 22 раза больше!

Думаете как выиграть в Гослото крупный приз – играйте в 5 из 36! Да, эта лотерея не накапливает большой джекпот, однако и шансы на выигрыш имеет значительно большие.

Вероятности в лотерее 5 из 36

Все вероятности совпадений количества выпавших чисел приводятся в таблице ниже:

Совпадений	Вероятность
0
1	1:3
2	1:9
3	1:82
4	1:2433
5	1:376992

Как рассчитать выигрышную комбинацию 5 из 36

Развернутая система – в погоне за 100% выигрышем джекпота

100% шанс на выигрыш в лотерею даст только развернутая система, в которую будут входить все 36 чисел, то есть ставка на все возможные комбинации. Однако такую ставку будет сделать не возможно и не разумно по нескольким причинам:

1. Ограничения по правилам. Количество выбранных чисел в развернутой ставке согласно правилам лотереи не превышает 11, оформить такую ставку в которой в одном билете будут зачеркнуты все числа нельзя.

2. Предположим, что кто-то вручную или автоматически всё же решится скупить все возможные комбинации на предстоящий тираж.

При стоимости билета в 80 рублей на это потребуется весьма существенная сумма в 30 159 360 рублей.

Такая ставка была бы вполне реализуема, если была бы логична её экономическая составляющая. Джекпот Гослото 5 из 36 никогда даже близко не подбирался к этой сумме, и никогда не подберется к этой сумме даже близко. Выигрыш джекпота при такой ставке конечно будет с вероятностью 100%, но сумма выигрыша по нему не покроет сумму необходимую потратить на покупку такого количества билетов.

Четыре развернутые системы – в погоне за выигрышем.

Все 36 чисел лотереи можно разложить поровну в четыре мешочка.

В каждом мешочке будет по 9 чисел. Всего же в ходе розыгрыша выпадает пять чисел.

Соответственно, если первые четыре выпавших чисел окажутся в разных мешочках, то пятое число окажется в одном из мешочков, в котором уже есть выпавшее число. То есть как ни крути при самом плохом варианте один из мешочков будет содержать 2 выигрышных числа, то есть окажется выигрышным.

Таким образом, чтобы гарантированно выиграть в лотерею, нужно сделать 4 развернутые системы, в которых будут задействованы все цифры.

Стоимость четырех таких ставок при сумме билета в 80 рублей будет равняться 40 320 рублям при гарантированном выигрыше равном 80 рублей.

Казалось бы, экономическая целесообразность такой ставки также сомнительна, но не надо забывать, что такая ставка может сорвать и приз более крупной категории, но здесь уже без каких либо 100% гарантий.

Так, вероятность совпадения трех чисел в такой ставке будет менее 30%, а вероятность выигрыша джекпота будет равна стандартной вероятности, как при покупке 504 билетов со случайными комбинациями.

Еще несколько систем игры в Гослото 5 из 36

Наша программа под названием Нострадамус пытается угадать выигрышную комбинацию ближайшего тиража на основе статистического анализа и других факторов, формируя лишь одну комбинацию.

Неполные системы 5 из 36 являются более щадящим по финансам аналогом развернутых систем. Многие игроки находят эту систему основной для своей игры.

Сбалансированная стратегия подвергает элементарному математическому анализу выпавшие комбинации.

Вывод

Лотерея остается лотереей – азартным увлечением, приносящее немногочисленным победителям миллионые выигрышы. В статье рассмотрены некоторые возможные методики выигрыша и теория вероятности в лотерее Гослото 5 из 36.

Основная формула комбинаторики

Пусть имеется k групп элементов, причем i-я группа состоит из n i элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n 1 *n 2 *n 3 *...*n k .

Пример 1. Поясним это правило на простом примере. Пусть имеется две группы элементов, причем первая группа состоит из n 1 элементов, а вторая - из n 2 элементов. Сколько различных пар элементов можно составить из этих двух групп, таким образом, чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли первый элемент из первой группы и, не меняя его, перебрали все возможные пары, меняя только элементы из второй группы. Таких пар для этого элемента можно составить n 2 . Затем мы берем второй элемент из первой группы и также составляем для него все возможные пары. Таких пар тоже будет n 2 . Так как в первой группе всего n 1 элемент, всего возможных вариантов будет n 1 *n 2 .

Пример 2. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
Решение: n 1 =6 (т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n 2 =7 (т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6), n 3 =4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4, 6).
Итак, N=n 1 *n 2 *n 3 =6*7*4=168.

В том случае, когда все группы состоят из одинакового числа элементов, т.е. n 1 =n 2 =...n k =n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно n k . Такой способ выбора в комбинаторики носит название выборки с возвращением.

Пример 3. Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8?
Решение. Для каждого разряда четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.

Рассмотрим множество, состоящие из n элементов. Это множество в комбинаторике называется генеральной совокупностью .

Число размещений из n элементов по m

Определение 1. Размещением из n элементов по m в комбинаторике называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.

Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.

Число размещений в комбинаторике обозначается A n m и вычисляется по формуле:

Замечание: n!=1*2*3*...*n (читается: "эн факториал"), кроме того полагают, что 0!=1.

Пример 5 . Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?
Решение: т.к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:

Определение 2. Сочетанием из n элементов по m в комбинаторике называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.

Пример 6 . Для множества {1, 2, 3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.

Число сочетаний из n элементов по m

Число сочетаний обозначается C n m и вычисляется по формуле:

Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся?

Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно:

Перестановки из n элементов

Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.

Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).

Число различных перестановок из n элементов обозначается P n и вычисляется по формуле P n =n!.

Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?

Решение: эта задача о числе перестановок семи разных книг. Имеется P 7 =7!=1*2*3*4*5*6*7=5040 способов осуществить расстановку книг.

Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно.

Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов).

Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны.

И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере.

Пример 9. На родительском собрании присутствует 20 человек. Сколько существует различных вариантов состава родительского комитета, если в него должны войти 5 человек?
Решение: В этом примере нас не интересует порядок фамилий в списке комитета. Если в результате в его составе окажутся одни и те же люди, то по смыслу для нас это один и тот же вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5.

Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок , которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5.

Задачи для самопроверки
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?

2. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?

3. В классе десять предметов и пять уроков в день. Сколькими способами можно составить расписание на один день?

4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?

5. Сколькими способами можно разложить восемь различных писем по восьми различным конвертам, если в каждый конверт кладется только одно письмо?

6. Из трех математиков и десяти экономистов надо составить комиссию, состоящую из двух математиков и шести экономистов. Сколькими способами это можно сделать?

Все N элементов, и ни один не повторяется, то это задача о количестве перестановок. Решение можно найти простым . На первом месте в ряду может стоять любой из N элементов, следовательно, получается N вариантов. На втором месте - любой, кроме того, который уже был использован для первого места. Следовательно, для каждого из N уже найденных вариантов есть (N - 1) вариантов второго места, и общее количество комбинаций становится N*(N - 1).
Это же можно повторить для остальных элементов ряда. Для самого последнего места остается только один вариант - последний оставшийся элемент. Для предпоследнего - два варианта, и так далее.
Следовательно, для ряда из N неповторяющихся элементов возможных перестановок равно произведению всех целых от 1 до N. Это произведение называется факториалом числа N и обозначается N! (читается «эн факториал»).

В предыдущем случае количество возможных элементов и количество мест ряда совпадали, и их число было равно N. Но возможна ситуация, когда в ряду меньше мест, чем имеется возможных элементов. Иными словами, количество элементов в выборке равно некоторому числу M, причем M < N. В этом случае задача определения количества возможных комбинаций может иметь два различных варианта.
Во-первых, может потребоваться сосчитать общее количество возможных способов, которыми можно выстроить в ряд M элементов из N. Такие способы называются размещениями.
Во-вторых, исследователя может интересовать число способов, которыми можно выбрать M элементов из N. При этом порядок расположения элементов уже не важен, но любые два варианта должны различаться между собой хотя бы одним элементом. Такие способы называются сочетаниями.

Чтобы найти количество размещений по M элементов из N, можно прибегнуть к такому же способу рассуждений, как и в случае с перестановками. На первом месте здесь по-прежнему может стоять N элементов, на втором (N - 1), и так далее. Но для последнего места количество возможных вариантов равняется не единице, а (N - M + 1), поскольку, когда размещение будет закончено, останется еще (N - M) неиспользованных элементов.
Таким образом, число размещений по M элементов из N равняется произведению всех целых чисел от (N - M + 1) до N, или, что то же самое, частному N!/(N - M)!.

Очевидно, что количество сочетаний по M элементов из N будет меньше количества размещений. Для каждого возможного сочетания есть M! возможных размещений, зависящих от порядка элементов этого сочетания. Следовательно, чтобы найти это количество, нужно разделить число размещений по M элементов из N на N!. Иными словами, количество сочетаний по M элементов из N равно N!/(M!*(N - M)!).

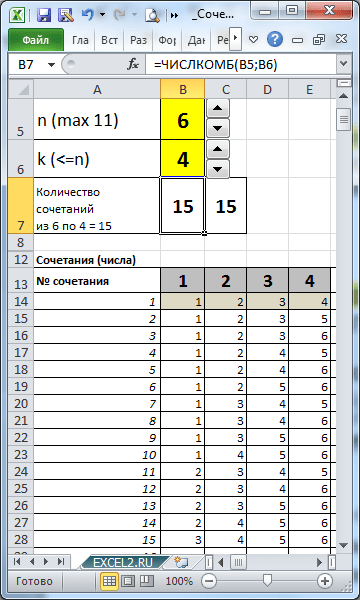
Подсчитаем в MS EXCEL количество сочетаний из n элементов по k. С помощью формул выведем на лист все варианты сочетаний (английский перевод термина: Combinations without repetition).

Сочетаниями из n различных элементов по k элементов называются комбинации, которые отличаются хотя бы одним элементом. Например, ниже перечислены ВСЕ 3-х элементные сочетания, взятые из множества, состоящего из 5 элементов {1; 2; 3; 4; 5}:

(1; 2; 3); (1; 2; 4); (1; 2; 5); (1; 3; 4); (1; 3; 5); (1; 4; 5); (2; 3; 4); (2; 3; 5); (2; 4; 5); (3; 4; 5)

Примечание : Это статья о подсчете количества сочетаний с использованием MS EXCEL. Теоретические основы советуем прочитать в специализированном учебнике. Изучать сочетания по этой статье - плохая идея.

Отличие Сочетаний от Размещений

Вывод всех комбинаций Сочетаний

В файле примера созданы формулы для вывода всех Сочетаний для заданных n и k.

Задавая с помощью количество элементов множества (n) и количество элементов, которое мы из него выбираем (k), с помощью формул можно вывести все Сочетания.

Задача

Автовоз может перевозить по 4 легковые машины. Необходимо перевезти 7 разных машин (LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo, Lada Largus). Сколькими различными способами можно заполнить первый автовоз? Конкретное место машины в автовозе не важно.

Нам нужно определить число Сочетаний 7 машин на 4-х местах автовоза. Т.е. n=7, а k=4. Оказывается, что таких вариантов =ЧИСЛКОМБ(7;4) равно 35.

Произвольным образом сопоставим маркам машин числовые значения и сделаем сокращения названий марок: LADA Granta (LG=1), Hyundai Solaris (HS=2), …